𝘚𝘭𝘰𝘸 𝘣𝘶𝘵 𝘴𝘵𝘦𝘢𝘥𝘺
A Tutorial on Spectral Clustering - 스펙트럴 클러스터링 본문
https://arxiv.org/abs/0711.0189
Von Luxburg, U. (2007). A tutorial on spectral clustering. Statistics and computing, 17, 395-416.
내용 정리
1. Introduction
Spectral clustering : 고유값을 사용한 그래프 기반 클러스터링
Spectrum : 행렬의 고유값들의 집합
⇒ 즉, 그래프의 스펙트럼을 분석하겠다는 의미
데이터의 feature값을 하나의 좌표로 생각하여 유클리디안 공간에서 클러스터링을 하는 k-means 클러스터링과 달리 연결 정보를 판단하는 그래프 기반의 스펙트럴 클러스터링을 사용하면 convex 모양의 클러스터 뿐만 아니라 더 복잡한 모양의 클러스터의 경우에도 쉽게 클러스터링을 진행할 수 있다.
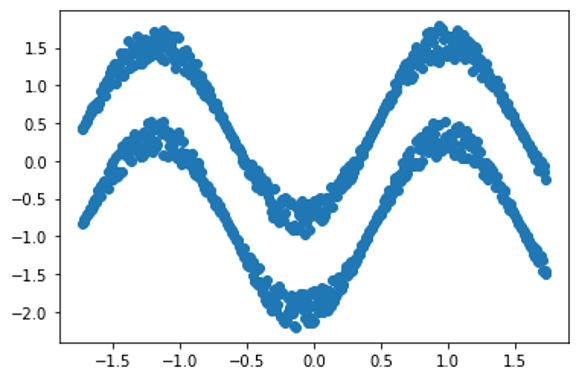
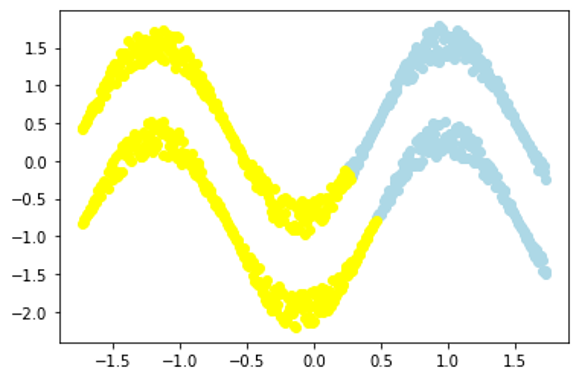
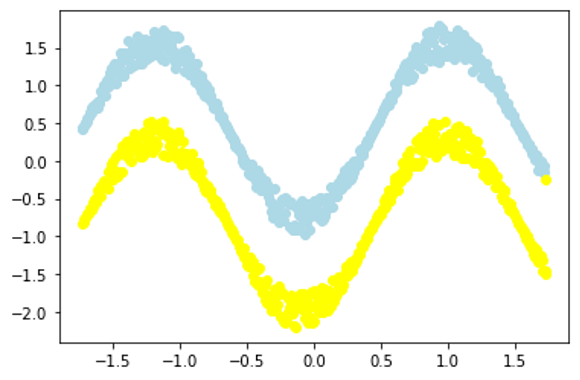
싸인함수 모양의 두 개의 클러스터에서 k-means를 적용했을 경우 가운데와 같이 클러스터가 나누어지는 반면, 스펙트럴 클러스터링을 적용하면 오른쪽 끝을 제외하고 올바르게 클러스터가 나누어진 것을 확인할 수 있다.
전반적인 내용을 이해하는 데 개인적으로 상당히 오래걸렸는데, spectral clustering을 간단하게 정리하면 다음과 같다.
- 유사도 그래프를 생성하고,
- 클러스터링을 쉽게 돌릴 수 있도록 유사도 행렬을 가공(라플라시안 행렬을 생성 → 고유값에 대한 고유벡터로 고유벡터에 대한 행렬을 생성)하여
- 생성된 새로운 행렬을 기반으로 k-means 클러스터링을 적용한다.
2. Similarity graphs
clustering의 목표는
- 비슷한 포인트들은 같은 그룹으로 묶이도록
- 비슷하지 않은 포인트들은 다른 그룹으로 묶이도록
데이터 포인트들을 여러 그룹으로 나누는 것이다.
유사도 외의 다른 정보가 없다면 데이터 표현으로 좋은 방식은 유사도 그래프 $G=(V,E)$를 형성하는 것이다. 그래프의 각 정점 $v_{i}$는 데이터 포인트 $x_{i}$에 해당되고, $x_{i}$와 $x_{j}$사이 일정 임계값 이상의 유사도 $s_{ij}$가 존재한다면 두 정점을 연결한다.
이렇게 설계된 유사도 그래프를 이용하여 clustering 문제를 해결 가능하다.
2.1 Different similarity graphs
클러스터링을 하기 전, 유사도 $s_{ij}$또는 거리 $d_{ij}$를 그래프로 변환하는 절차이다.
데이터 포인트 간 근접한 이웃관계를 모델링 하는 것이 목적으로, spectral clustering에서 가장 많이 쓰이는 3가지 방법이 소개된다.
- ε-neighborhood graph
임계값 ε보다 더 가까운 거리에 있는 모든 포인트를 연결한다. - $k$-nearest neighbor graphs(kNN 그래프)
$v_{j}$가 $v_{i}$의 $k$번째 가까운 이웃 중 하나일 때 두 정점을 연결한다. 이 때, 이웃 관계는 대칭의 형태가 아닐 수 있기 때문에 방향 그래프로 고려되는데, 대칭 행렬 형태의 유사도 행렬을 만들기 위해 무향 그래프로 만든다.
- $k$-nearest neighbor graph
$v_{j}$가 $v_{i}$의 kNN이거나 $v_{i}$가 $v_{j}$의 $k$NN일 때 연결 - mutual $k$-nearest neighbor graph
둘 다 서로의 $k$-nearest neighbor일 때만 연결
- $k$-nearest neighbor graph
- Fully connected graph
양의 유사도를 갖는 정점 전부를 연결한다. 그래프는 근접한 이웃 관계를 표현해야 하나 이 방법은 모든 노드가 연결될 수 있기 때문에 유사도 함수가 근접한 이웃관계를 모델링할 경우에만 유용하다.
ex) Gaussian similarity function
$$ s(x_{i} ,x_{j})=e^{-\frac{||x_{i} - x_{j}||^2}{(2\sigma)^2}} $$
$\sigma$는 $\varepsilon$-neighbor graph에서의 $\varepsilon$과 유사한 역할을 한다.
3. Graph Laplacians and their basic properties
라플라시안 그래프는 spectral clustering에서 가장 핵심이 되는 tool이라 할 수 있다.
수학적인 내용이 매우 어렵기 때문에.... 하나하나 이해하는 것 보다 몇 가지 특성만 기억하는 것이 좋을 것 같다.
표기법
- $W$ : 가중치 인접 행렬
- $D$ : 그래프의 포인트 별 연결된 edge의 각 가중치를 합한 차수행렬
3.1 The unnormalized graph Laplacian
정규화되지 않은 라플라시안 그래프는 다음과 같이 정의한다.
$$L=D-W$$
위와 같이 정의된 행렬 $L$은 다음과 같은 성질을 만족한다.
- 모든 벡터 $f \in \mathbb{R}^n$에 대해 다음 식을 만족한다.
$$ f'Lf=\frac{1}{2} \sum_{i,j=1}^n w_{ij}(f_{i}-f_{j})^2$$ - $L$은 대칭행렬이고 양의 준정부호(positive semi-definite) 행렬이다.
- $L$은 항상 0을 가장 작은 고유값으로 가지고, 이에 해당하는 고유벡터 $u$는 constant one vector이다.
$$u=\begin{bmatrix}1&1&\ldots&1\end{bmatrix} ^T$$ - $L$은 음수가 아닌 실수 고유값을 가진다.
$$ 0=\lambda_{1} \leq \lambda_{2} \leq \cdots \leq \lambda_{n} $$
인접행렬 $W$는 block diagonal 형태이고, $D$ 역시 대각행렬이기 때문에 $L$은 block diagonal 형태가 된다.
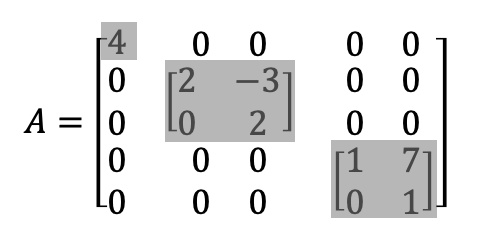
이러한 block diagonal의 $L$이 다음과 같은 형태라고 간단히 표현할 수 있을 때,
$$L= \begin{bmatrix}L_{1} & && \\ & L_{2} \\&&\ddots& \\&&&L_{k} \end{bmatrix} $$
각 $L_{i}$들은 sub-Laplacian이라고 할 수 있다.
모든 $L_{i}$는 고유값 0을 하나씩 갖기 때문에(다중도가 1이라는 성질), $L$은 $k$개의 고유값을 가진다.
3.2 The normalized graph Laplacian
각 항을 차수로 나눠주어 정규화한 라플라시안 그래프는 차수를 나눠주는 방식에 따라 $L_{sym}$ 또는 $L_{rw}$ 두가지로 나눌 수 있다.
각각의 정의는 다음과 같다.
1. Symmectric graph Laplacian
$$L_{sym}:= D^{-1/2}LD^{-1/2}=I-D^{-1/2}WD^{-1/2}$$
이고, 행렬의 각 원소는 다음과 같은 성질을 만족한다.
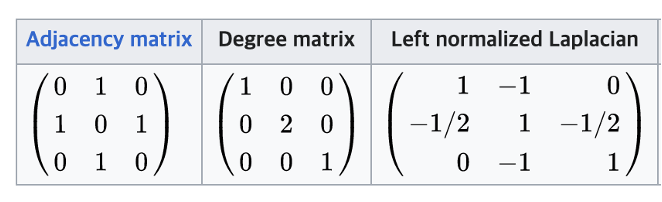
$$ L_{sym} =\begin{cases}1 & i=j\\ -\frac{1}{\sqrt{deg(v_{i})deg(v_{j})}} & i \neq j, v_{i} \,is\, adjacent\,to\, v_j\\0 & otherwise\end{cases} $$

2. Random walk graph Laplacian
$$L_{rw}:=D^{-1}L=I-D^{-1}W$$
$$L_{rw}=\begin{cases}1 & i=j\\ -\frac{1}{\deg(v_i)} & i \neq j, v_{i} \,is\, adjacent\,to\, v_j\\0 & otherwise\end{cases} $$
4. Spectral clustering algorithms
spectral clustering은 어떤 라플라시안 그래프를 사용했는가에 따라 unnormalized spectral clustering과 normalized spectral clustering 두가지로 나눌 수 있다.
사용하는 그래프 제외 작동 방식은 모두 동일하므로 정규화되지 않은 스펙트럴 클러스터링 알고리즘을 중심으로 설명한다.
Unnormalized spectral clustering
- 주어진 유사도 그래프를 바탕으로 $L=D-W$를 이용하여 Laplacian 행렬 $L$ 연산
$$ L= \begin{bmatrix}L_1&\cdots&0 \\ \vdots&\ddots&\vdots \\ 0&\cdots&L_k\end{bmatrix}$$ - $L$의 처음 $k$개의 고유벡터(고유값이 0에 해당하는 고유벡터) $u_1,u_2,\ldots,u_k$ 연산
- 벡터 $u_1,u_2,\ldots,u_k$로 구성된 행렬 $U$ 생성
$$U= \begin{bmatrix} |&|&&| \\ u_1&u_2&\cdots&u_k \\ |&|&&| \end{bmatrix} $$ - 행렬 U의 각 행벡터 $v_1,v_2,\cdots,v_n$ 선택
- $v_1,v_2,\cdots,v_n$ 클러스터링($k$-means 알고리즘 이용)
Normalized spectral clustering은 어떤 정규화된 라플라시안을 사용했는가에 따라 두가지로 분류한다.


$L_{sym}$을 사용한 두번째 방법의 경우, 이와 같이 연산된 고유벡터는 고유값 별 각기 다른 값을 갖기 때문에 추가적으로 행 정규화 단계가 시행된다.
5. Graph cut point of view
클러스터링은 서로 다른 그룹들을 분리하고자 한다. 따라서 유사도 그래프를 형성할 때
- 다른 그룹들간의 edge는 매우 낮은 가중치를 가지도록(external separation)
- 그룹 내에서의 edge는 매우 높은 가중치를 가지도록(internal cohesion)
그래프를 분할하고자 한다.
이러한 문제의 가장 단순하고 직접적인 해결 방법은 바로 mincut 문제를 해결하는 것이다.
Mincut approach?
$$cut(A_1, \cdots, A_k) := \frac{1}{2} \sum_{i=1}^k W(A,\bar{A})$$
즉, 클러스터들 사이에 연결된 edge들의 가중치의 합이 최소화되는 partition을 선택하는 문제로, 가장 많이 사용되는 목적함수로는 RatioCut과 Ncut(Normalized Cut)이 있다.
1. RatioCut
subset $A$의 크기는 정점의 수 $|A|$로 결정한다.
$$ RatioCut(A_1,\ldots,A_k):=\frac{1}{2} \sum_{i=1}^k \frac{W(A_i, \bar{A_i})}{|A_i|} \\= \sum_{i=1}^{k} \frac{cut(A_i, \bar{A_i})}{|A_i|}$$
2. Ncut
subset $A$의 크기는 가중치의 합 $vol(A)$로 결정한다.
$$Ncut(A_1, \ldots, A_k):= \frac{1}{2} \sum_{i=1}^k \frac{W(A_i, \bar{A_i})}{vol(A_i)} = \sum_{i=1}^k \frac{cut(A_i, \bar{A_i})}{vol(A_i)}$$
두 목적함수는 클러스터의 목적을 달성할 수 있게 하지만, NP-hard 문제에 속한다.
따라서 문제를 근사하여 해결하도록 한다.
5.1 Approximating RatioCut for $k=2$
목표 : $\min_{A\subset V}RatioCut(A,\bar{A})$
하나의 그래프를 두 클러스터 $A$와 $\bar{A}$로 분리하는 것
여러 차원의 데이터 포인트 $v_i$를 하나의 실수값 $f_i$로 매핑하는 과정을 다음과 같이 정의한다.
$$f=\begin{cases} \sqrt{\frac{|\bar{A}|}{|A|}} \,if\, v_i \in A\\ -\sqrt{\frac{|A|}{|\bar{A}|}} \,if\,v_i\in \bar{A} \end{cases}$$
이렇게 정의된 $f=(f_1,...,f_n)'$을 라플라시안 그래프의 성질에 이용하면
이러한 증명을 통해 $\min_{A\subset V}RatioCut(A,\bar{A})$ 문제는 $\min_{f\in \mathbb{R}^n}f'Lf$로 근사가 가능하다.
따라서 $f'Lf$를 최소화하는 벡터 $f$를 찾는 것을 목표로 문제를 해결한다.
이 때의 $f$는 Rayleigh-Ritz 알고리즘에 의해 $L$의 두번째로 작은 고유값의 고유벡터가 된다.
(여기서의 $L$의 가장 작은 고유값은 0인데, 라플라시안 성질에 의해 그에 대응하는 고유벡터는 1벡터($\begin{matrix}[1&1&...&1]\end{matrix}$)이기 때문)
즉, $L$의 두번째 고유벡터로 $RatioCut$을 대략 최소화할 수 있다.
이렇게 구한 $f$를 지시 함수로서 사용하여 클러스터링을 쉽게 적용할 수 있다.
$$\begin{cases}v_i \in A, \,if\,f_i \geq 0 \\ v_i \in \bar{A}, \,if\, f_i<0 \end{cases}$$
위의 과정을 예시로 들면 다음 그림과 같다.

그래프 하나에 대하여 $L$를 정의하여 그에 따른 고유값과 고유벡터를 구한 다음
두번째 고유벡터 $\begin{matrix}[0.3&0.6&0.3&-0.3&-0.3&-0.6]^T\end{matrix}$로 k-means clustering을 진행하면
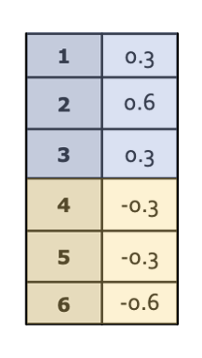
위와 같은 결과로 클러스터링이 완료될 것이다.
5.2 Approximating RatioCut for arbitrary $k$
$k$가 2보다 큰 모든 경우에 적용할 수 있는 5.1의 일반화된 경우이다.
목표 : $\min_{A_1,...A_k}RatioCut(A_1,...,A_k)$
전체 데이터를 $k$개의 클러스터 $(A_1,A_2,...,A_k)$로 분리하고자 한다.
데이터들의 전체 집합 $V$를 $k$개의 클러스터로 나눈 partition을 $A_1, ... ,A_k$라고 할 때, $k$개의 지시벡터 $h_j=(h_{1,j},h_{2,j},...,h_{n,j})'$는 다음과 같이 정의한다.
$$h_{i,j} = \begin{cases} \sqrt{\frac{1}{|A_j|}} \quad if\,v_i \in A_j\\0 \quad otherwise \end{cases}$$
즉, 전체 행렬 $H$는 $k$개의 지시벡터를 열벡터로 갖는 행렬로 정의가 가능하다.
정의된 행렬 $H$를 라플라시안 성질에 이용하면
$k=2$일 때와 마찬가지로 $\min_{A_1,...A_k}RatioCut(A_1,...,A_k)$를 $\min_{H\in \mathbb{R}^{n\times k}} \textrm{Tr}(H'LH)$로 근사할 수 있는데, 이러한 $H'LH$의 대각합을 최소화하는 행렬 $H$는 $L$의 첫 $k$개의 고유벡터에 해당한다.(4번 알고리즘 설명 단계에서의 $U$ 행렬)
예를 들어, $k=3$일 때의 행렬 $L$과 그에 따른 첫 $k$개의 고유벡터는 다음과 같다.
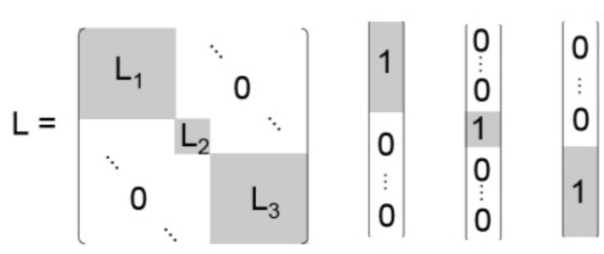
이 때 세개의 고유벡터 행렬 $H$로부터 각 행별 k-means 클러스터링을 진행하면 $n$개의 데이터들이 각각 3개의 클러스터에 할당될 것이다.
조금 더 자세한 예시로 다음과 같은 데이터셋으로부터 인접 그래프를 생성하고, 인접행렬로 정의된 라플라시안 행렬이 다음과 같다고 한다.

위의 라플라시안 행렬의 고유값과 고유벡터를 구하면 다음과 같이 나오는데,
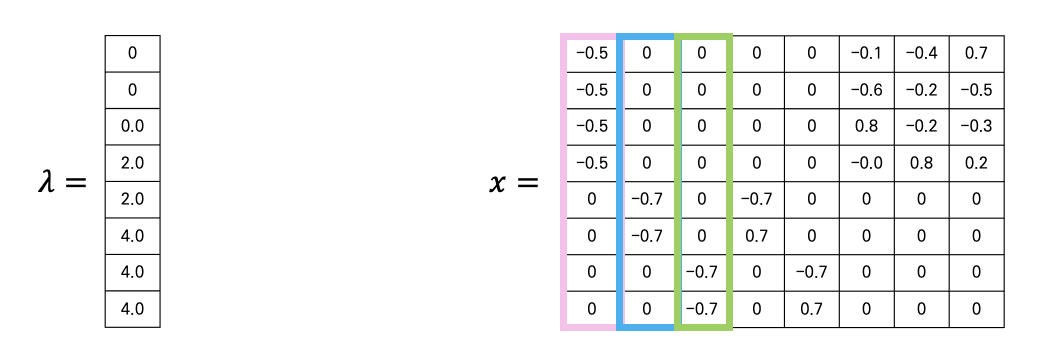
이 때 고유값이 0인 첫 3개의 고유벡터로 클러스터링을 진행하게 되면 위의 그래프와 유사하게 올바른 클러스터링 결과가 나올 것임을 예상할 수 있다.(고유벡터 행렬에서 지시벡터들의 값이 1이 아닌 이유는 파이썬에서 numpy로 고유벡터를 계산할 때 열별로 정규화를 하여 나오기 때문에...그냥 연산하면 고유값이 0인 고유벡터들은 모두 0과 1로 이루어진 지시벡터의 성향을 띠는 것이 맞다..ㅠㅠ)
5.3 Approximating Ncut
RatioCut과 유사하게 작동하나, 그래프에서의 인접 노드 수로 연산하는 것이 아닌 가중치로 연산하는 점이 다르다.
$k=2$에서, 매핑함수 $f$는 다음과 같이 정의한다.
$$f_i=\begin{cases} \sqrt{\frac{vol(\bar{A})}{vol(A)}} \quad if\, v_i \in A\\ -\sqrt{\frac{vol(A)}{vol(\bar{A})}} \quad if \, v_i \in \bar{A}\end{cases}$$
Ncut 최소화는 $min_A f'Lf$와 동일한 문제이다.
여기서 $f$는 $L_{rw}$의 두 번째 고유벡터이고, $g:=D^{1/2}f$라고 정의할 때, $g$는 $L_{sym}$의 두 번째 고유벡터이다.
$k>2$에서 지시벡터 $h_{i,j}$는 다음과 같이 정의한다.
$$h_{i,j}=\begin{cases} \frac{1}{\sqrt{vol(A_j)}} \quad if\, v_i \in A_j \\0 \quad otherwise\end{cases}$$
$H$는 $k$개의 지시벡터를 열벡터로 갖는 행렬이고,
$min_{A_1,...,A_k} \textrm{Tr}(H'LH)$는 $min_{T\in \mathbb{R}^{n \times k}} \textrm{Tr}(T'D^{-1/2}LD^{-1/2}T), T=D^{1/2}H$로 근사하여 해결할 수 있다.
$L_{sym}$의 고유벡터 $k$개로 구성된 행렬 $T$에 의해 대각합을 최소화할 수 있고, $H=D^{-1/2}T$로 대체하여 $L_{rw}$에서의 문제를 해결할 수 있다.
5.4 Comments on the relaxation approach
당연한 얘기지만, 이렇게 근사하는 방법이 정확한 solution이라는 보장은 없다. 실제 RatioCut의 정답이 $A_1, A_2,...,A_k$이고, 클러스터링의 결과가 $B_1,B_2,...,B_k$라고 가정했을 때, $RatioCut(B_1,B_2,...B_k)-RatioCut(A_1,A_2,...,A_k)$의 클 수도 있다는 의미이다. 그렇다면 왜 근사하여 푸는 것일까?
풀기 간단한 표준적인 선형대수 문제로 해결할 수 있기 때문에 이러한 방법을 사용한다.
'machine learning' 카테고리의 다른 글
| BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding - BERT 바닥까지 이해하기 (1) | 2025.02.24 |
|---|