𝘚𝘭𝘰𝘸 𝘣𝘶𝘵 𝘴𝘵𝘦𝘢𝘥𝘺
[알고리즘] 누적 합(prefix sum) 본문
1. 누적 합(prefix sum)
1.1 개념
특정 배열에서 어떠한 구간까지의 합을 구하는 방식. 어떠한 1차원 배열 [ 1, 5, 2, 10, 1, 8 ] 에서 가장 합이 큰 길이가 3인 부분 배열을 고를 때, [ 1, 5, 2 ], [ 5, 2, 10 ], ... , [ 10, 1, 8 ] 을 하나하나씩 반복문을 돌려나가면서 비교해 나가는 것이 아니라 미리 누적합을 계산해둔 배열 [ 1, 6, 8, 18, 19, 27 ] 를 활용하여 계산을 하기 때문에, 계산량에서 큰 이득이 있다.
1.2 1차원 배열
알고리즘 작동 방식은 다음과 같다.
1. 길이가 N(또는 N + 1)의 누적합 배열을 선언하고, 각 누적합 배열의 i번째 인덱스에는 원본 배열의 1번째부터 i번째 원소의 합을 저장한다.
2. a번째 원소부터 b번째 원소(1 ≤ a ≤ b ≤ N)까지의 누적합을 구하고 싶을 때, 구하는 방식은
b번째 누적합 값에서 (a - 1)번째 누적합 값을 빼서 구한다.

그림의 예시와 같은 배열에서
3번째 원소(6)에서 6번째 원소(1)까지의 누적합을 구하는 방법은
prefix_sum[5] - prefix_sum[1] = 23 - 6 = 17

[a]부터 [b]까지의 합은 1 ~ b까지의 합에서 겹치는 부분인 1 ~ (a-1) 을 빼주면 되기 때문에,
미리 정의된 배열만 있으면 O(1)만에 계산이 가능한 간단한 원리의 알고리즘이다.
1.2.1 코드
int N, a, b; // predefined
vector<int> A(N); // predefined
vector<int> prefix_sum(N + 1, 0);
for(int i = 1; i <= N; i++) {
prefix_sum[i] = prefix_sum[i - 1] + A[i - 1];
}
// a ~ b까지 구간합
sum = prefix_sum[b + 1] - prefix_sum[a];
1.3 2차원 배열
사실 이 포스팅을 하게 된건 2차원 배열의 누적합 때문에...
2차원 배열에서의 누적합은 1차원 배열에서의 원리와 동일하다.
다만, 누적합 배열을 만들어주는 방식에서부터 조금 생각을 해줘야 한다.
2차원 배열의 누적합 배열을 만들어 줄때는 (0, 0) ~ (i, j) 까지의 직사각형 배열 내 누적합을 구해준다는 생각으로 계산을 해주면 된다.
(0, 0) ~ (i, j)까지의 누적합은 다음과 같이 구한다.
[ (0, 0) ~ (i, j - 1)까지의 누적합 + (0, 0) ~ (i - 1, j)까지의 누적합 + (i, j)의 배열값 ] - [ (0, 0) ~ (i - 1, j - 1)까지의 누적합 ]
그리고 (a, b) ~ (c, d) 사이의 누적합은 다음과 같이 구한다.
[ (c, d)까지의 누적합 + (a - 1, b - 1)까지의 누적합 ] - [ (a - 1, d)까지의 누적합 + (c, b - 1)까지의 누적합) ]
다음과 같이 0과 1로 이루어진 배열 A[][]가 있다고 할 때, (3, 2)까지의 누적합은 3이 된다.
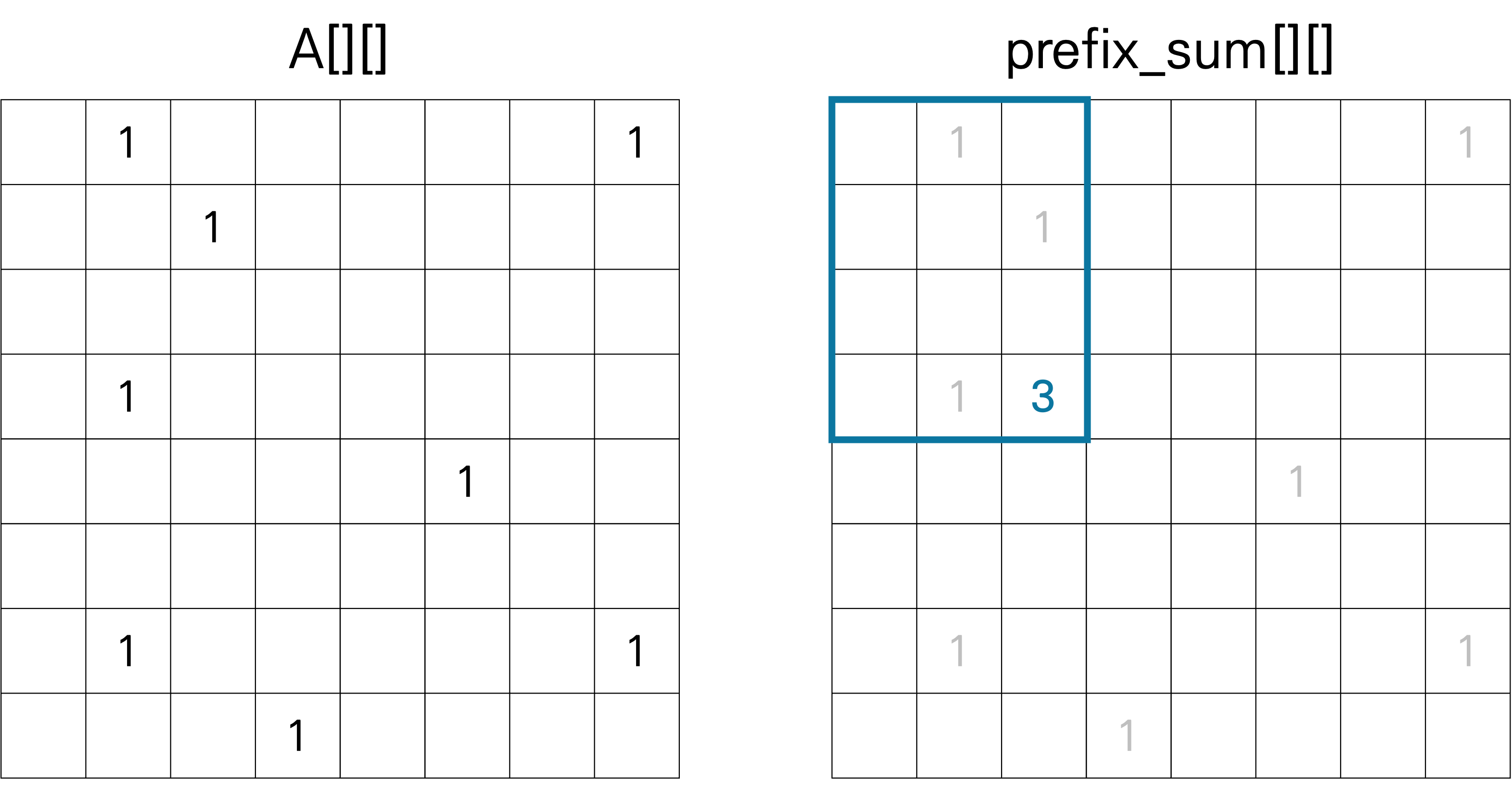
누적합 배열에서 (3, 2)를 이루는 값은 다음과 같이 구한다.
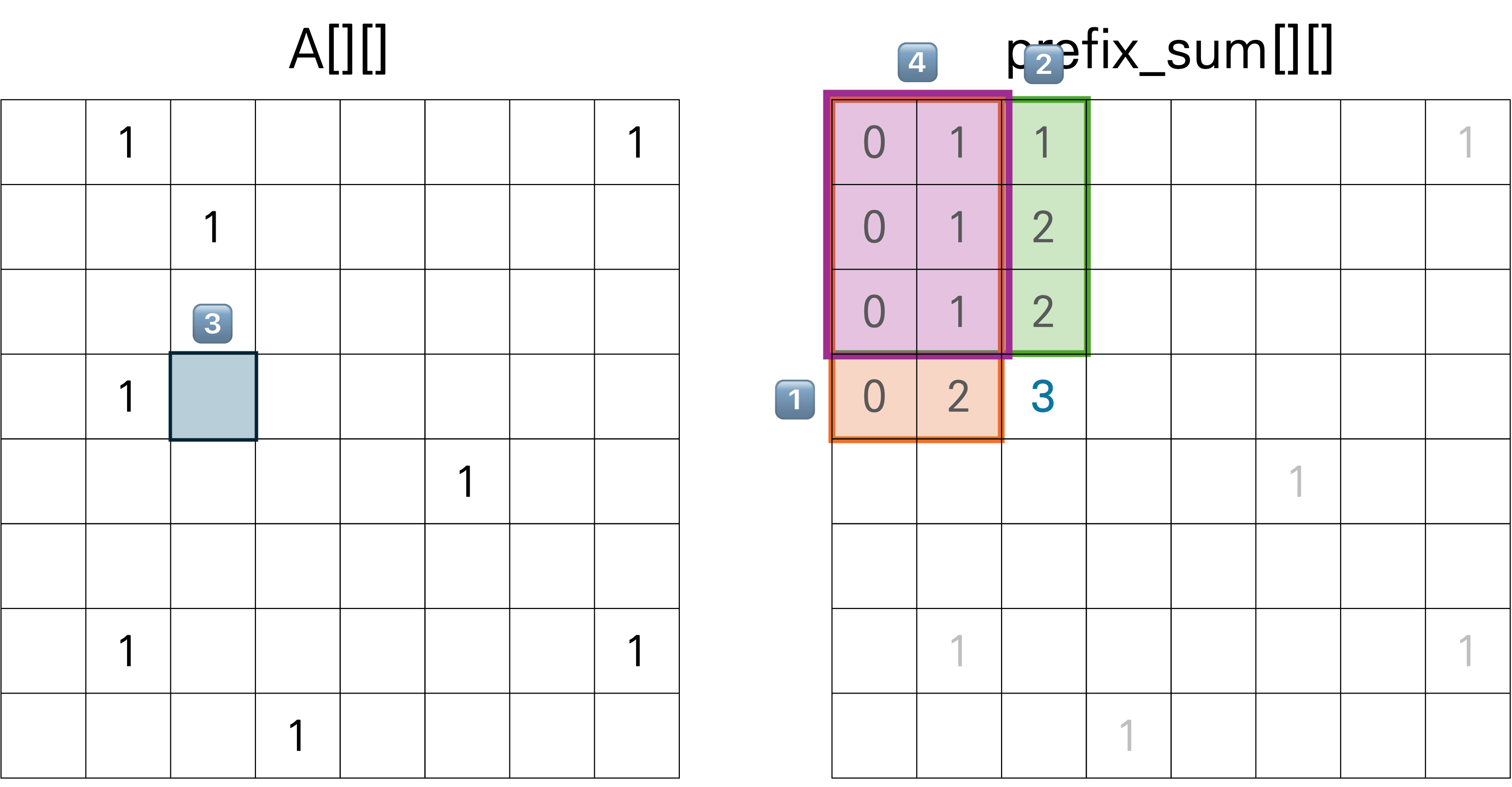
1️⃣ (0, 0) ~ (3, 1) 까지의 누적합
+ 2️⃣ (0, 0) ~ (2, 2) 까지의 누적합
+ 3️⃣ (3, 2)에서의 배열 값(여기서는 0)
- 4️⃣ 겹치는 구간((0, 0) ~ (2, 1) 까지의 누적합)
을 모두 계산해주면 1️⃣ 2 + 2️⃣ 2 + 3️⃣ 0 - 4️⃣ 1 = 3 이 된다.
이런 식으로 누적합 배열을 모두 계산해주면 다음과 같다. (정신없음)
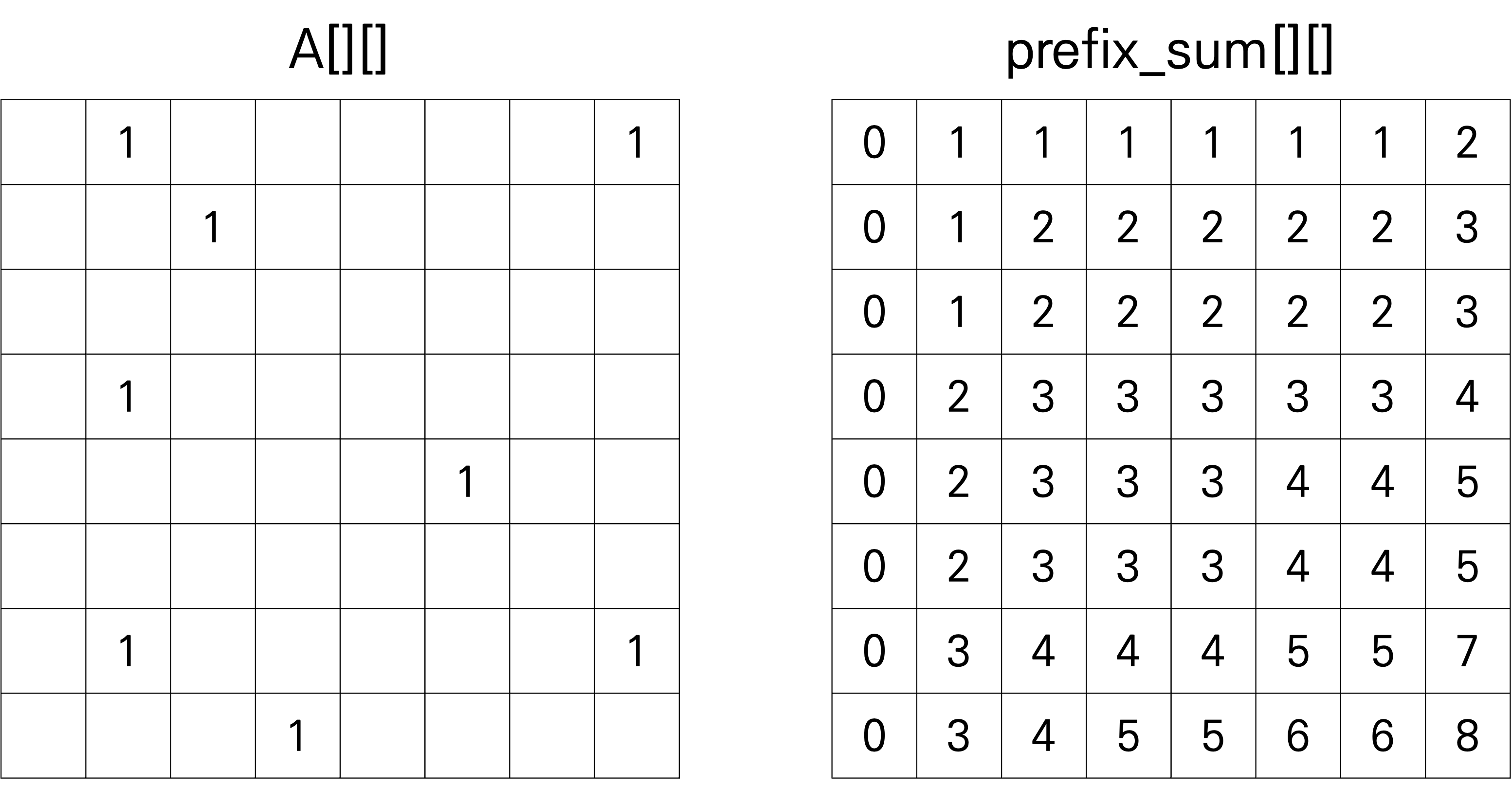
그럼 여기서 (a, b) ~ (c, d) 까지의 누적합을 구하는 방식은 앞선 방식과 마찬가지로 다음과 같이 구한다.
(3, 1) ~ (6, 5) 까지의 누적합이 궁금할 때,
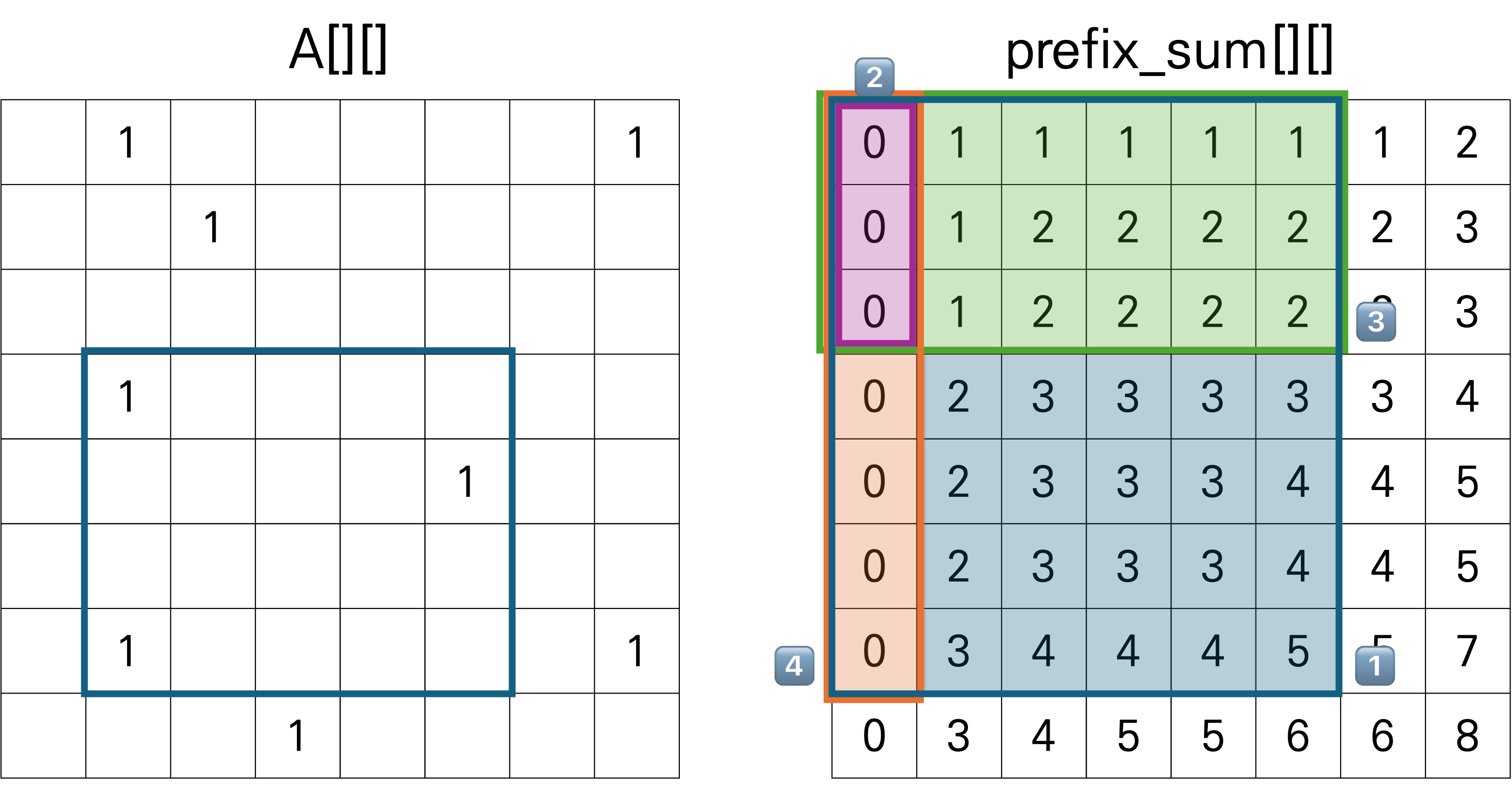
1️⃣ (0, 0) ~ (6, 5) 까지의 누적합
+ 2️⃣ 두번 빼지는 구간((0, 0) ~ (2, 0) 까지의 누적합)
- 3️⃣ (0, 0) ~ (2, 5) 까지의 누적합
- 4️⃣ (0, 0) ~ (6, 0) 까지의 누적합
을 모두 계산해주면 1️⃣ 5 + 2️⃣ 0 - 3️⃣ 2 - 4️⃣ 0 = 3 이 된다.
1.3.1 코드
int N, a, b, c, d; // predefined
vector<vector<int>> A(N, vector<int>(N)); // predefined
vector<vector<int>> prefix_sum(N, vector<int>(N + 1, 0));
for(int i = 1; i <= N; i++)
for(int j = 1; j <= N; j++)
prefix_sum[i][j] = A[i - 1][j - 1] + prefix_sum[i][j - 1]
+ prefix_sum[i - 1][j] - prefix_sum[i - 1][j - 1];
sum = prefix_sum[c + 1][d + 1] - prefix_sum[a][d]
- prefix_sum[c][b] + prefix_sum[a][b]
누적 합 사용해서 풀어야했던 문제
🔗 구름-놀이공원
'알고리즘' 카테고리의 다른 글
| [알고리즘] 이분 탐색(Binary Search) (0) | 2021.08.08 |
|---|---|
| [알고리즘] 그래프 순회 문제 - 2. 너비 우선 탐색(BFS) (0) | 2021.07.22 |
| [알고리즘] 그래프 순회 문제 - 1. 깊이 우선 탐색(DFS) (0) | 2021.07.21 |
| [알고리즘] 정렬 - 2. 퀵 정렬(Quick Sort) (0) | 2021.07.15 |
| [알고리즘] 정렬 - 1. 병합 정렬(Merge Sort) (0) | 2021.07.14 |




